Club de Rubik de Catalunya

TUTORIAL DE BLINDFOLD PER A PRINCIPIANTS

Fer Blindfold no és una qüestió només al abast dels experts en el cub de Rubik. En realitat, per a fer-ho amb un mètode senzill, que és el que explicaré en els següents paràgrafs, només s'ha de tenir paciència, interès, una mica de concentració, i coneixements bàsics cobre al resolució del cub de Rubik. Personalment, crec que aquest mètode és ideal per a apendre a fer Blindfold. Tanmateix, és veritat que existeixen altres mètodes més ràpids per a fer Blindfold, i a al vegada considerablement més complicats, tot i que amb aquest mètode es poden arrivar a assolir temps per sota dels 5 minuts. Aquest temps, comença desde el primer contacte visual amb el cub, és a dir, s'incloeixen tant la memorització com la resolució del cub.

Coneixements previs

Per a fer Blindfold amb aquest mètode no fa falta saber gaires algorismes, sinó que basta unicament amb saber un algorisme per a orientar vèrtex, un altre per a orientar arestes i la permutació "T". La majoria dels que resolen el cub amb el mètode per a principiants estan familiaritzats amb l'orientació de vèrtex, tot i això, pot ser que no coneguin la permutació "T". Més endavant faré referència a ambdós algorismes.

El mètode

El mètode consisteix en dues etapes bàsiques:

• Memorització
• Execució

L'Execució, alhora, es divideix en 4 subetapes:

• Orientació de arestes
• Orientació de vèrtex
• Permutació de arestes
• Permutació de vèrtex

Definició de orientació

Posem l'exemple d'un cub amb el color blanc a la cara superior, i el color vermell a la cara frontal. Quan es veu un cub resolt desde uan posició com la mencionada, podem percebre inmediatament que cada a peça li correspon una posició definida. D'aquesta manera, l'aresta blanca/vermella ha de estar entre el centre blanc i el vermell; el vèrtex groc/taronja/verd ha de estar sempre entres els centres groc, taronja i verd, i així successivament.
Tanmateix, es pot percebre que totes les peces poden girar-se sobre elles mateixes sense alterar la seva posició. Les arestes, donçs, poden estar girades només d'una forma, mentre que els vèrtex poden estar girats tan en sentit horari com en sentit antihorari. Al gir que realitzen les peces del cub sobre elles mateixes l'anomenarem canvi en la seva orientació. Per a canviar la orientació tant de vèrtex com de arestes sense alterar la seva posició, hem de tenir en compte que:

• Poden orientar-se 3 vèrtex en sentit horari al mateix temps
• Poden orientar-se 3 vèrtex en sentit antihorari al mateix temps
• Poden orientar-se 2 arestes la orientació dels quals es contraria (horaria/antihoraria) al amteix temps
• Les arestes s'orienten en nombres parells

Definir si una peça o varies està/n ben o mal orientada/es

Per a definir si una peça està ben o mla orientada, el primer que hem de fer es triar uan cara superior i una cara frontal. Jo, per exemple, sempre utilitzo la cara vermella com a cara superior i la cara blanca com a cara frontal. La configuració que utilitzo donçs seria:

U: vermella

F: blanca

L: blava

R: verda

D: taronja

B: groga

Amb això tenim que:
a) Un vèrtex està ben orientat si el seu color corresponent a les cares "U" o "D" es troba donçs a les cares "U" o "D". Si aquest color es troba mirant a una altra cara, per exemple "R" o "B", aleshores sabem que el vèrtex en qüestió està mal orientat i per tant que necessita un gir sobre ell mateix o un canvi en la seva orientació. En el meu cas, els meus vèrtex estan ben orientats si i només si el color corresponent a les cares "U" o "D", és a dir, el vermell o el taronja es troba mirant a les cares vermella o taronja.

Ara tenim dos tipus de arestes: les que tenen un color corresponent a "U" o "D", (en el meu cas arestes que tinguin vermell o taronja), i les que no el tenen. Aleshores tenim que:
b) Una aresta que SI tingui en un dels seus costats un dels colors corresponents a "U" o "D" està ben orientada (en el cas que aquesta aresta es trobi a la cara superior o inferior) si aquest color apunta a "U" o "D". En el cas que aquesta aresta es trobi a al capa del mig, i per obvietat cap de les dues cares apunti a "U" o "D", es trobarà ben orientada si el color de aquestes cares apunta a "R" o "L".
c) Una aresta que NO tingui en cap dels seus costats un color corresponent a "U" o "D" està ben orientada ( en el cas que aquesta aresta estigui a les cares "F" o "B") si en un dels costats, el color que correspon a "F" o "B" apunta a "F" o "B". En el cas que aquestes arestes no es trobin ni a la capa frontal ni a la posterior, sinó a la capa intermedia, aquestes es trobaran ben orientades si el color de "F" o "B" apunta a "R" o "L".

Com que resulta difícil entendre això amb paraules, ho ilustraré seguidament:

La següent ilustració denota la correcta orientació dels vèrtex, èssent la part iluminada el costat dels vèrtex en el qual es troba el color corresponent a "U" o "D".

La següent il·lustració denota la correcta orientació de les arestes, èssent la part iluminada el costat de les arestes en el qual es troba el color corresponent a "U" o "D".

La següent il·lustració denota la correcta orientació de les arestes que NO tenen un color corresponent a "U" o "D" (punt c). La part iluminada mostra, donçs, el color corresponent a "F" o "B".

Definició de permutació

Definirem permutació de uan manera simple, ja que per a aquest mètode no s'ha de entendre gran cosa. Anomenem permutació al canvi de posició que es realitza sobre un determinat nombre de peces. En aquest mètode el cub es va construint "peça per peça", permutant amb la permutació "T".

Enumeració del cub

Sabent donçs, com ja havia explicat anteriorment, el fet que cada a cada peça li correspon una determinada posició definida, podem agafar un cub, posar-lo en una determinada posició (jo per exemple, col·loco la cara vermella a dalt i la blanca davant), i començar a enumerar les peces. Amb quina finalitat? La resposta és simple; enumerant les peces, tant la memorització com la execució poden tornar-se més senzilles.

Enumeració d'arestes:                     Enumeració de vèrtex:

1 : UL (upper left)                            
2 : UF (upper front)
3 : UR (upper right)                           1 : UFL (upper front left)
4 : UB (upper back)                           2 : UFR (upper front right)
5 : FL (front left)                                  3 : UBR (upper back right)
6 : FR (front right)                               4 : UBL (upper back left)
7 : BR (back right)                              5 : DFL (down front left)
8 : BL (back left)                                 6 : DFR (down front right)
9 : FD (front down)                             7 : DBR (down back right)
10 : DR (down right)                          8 : DBL (down back left)
11 : DB (down back)
12 : DL (down left)

Algorismes

Bé, donçs tot seguit mostraré els algorismes que faran servei en la resolució del cub. Recomano a tots aquells que mai hagin vist els algorismes que ara ensenyaré, que els practiquin diversos cops abans de intentar resoldre el cub a cegues. De veritat, és molt frustrant fallar un intent de Blindfold perquè no es té ben mecanitzat algun moviment.
 

• Permutació "T":  R U R’ U’ R’ F R2 U’ R’ U’ R U R’ F’    

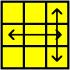
• M U M U M U2 M’ U M’ U M’ U2  Aquest algorisme canvia l'orientació de 2 arestes oposades.

• M U M U M U M U M’ U M’ U M’ U M’ U  Aquest algorisme canvi l'orientació de 4 arestes de una mateixa cara.

• Orientació de vèrtex. Els que resolen el cub per el mètode de principiants saben a què em refereixo amb ''canvia l'orientació d'una peça sense alterar la seva posició"

  Per a canviar 3 vèrtex a la mateixa capa en sentit horari:
  (Considerar que A= (R’ D R D’)2) A U A U A U2

  Per a canviar 3 vèrtex a la mateixa capa en sentit antihorari:
  (Considerar que B= (R’ D’ R D)2) B U B U B U2

  Girar 2 vèrtex oposats: R’ D’ R D R’ D’ R U’ R’ D R D’ R’ D R U

  Per a canviar 2 vèrtex a la mateixa capa adjacents mira el 7è pas del mètode de principiants.

Fins ara no he fet més que explicar en breu la teoria del mètode. Un cop s'ha comprès tot bé, podem continuar a explicar la pràctica, per descomptat, amb un exemple.

SCRAMBLE

Cara vermella a dalt, blanca davant: L R D U F2 B2 U2 L2 B2 L’ B2 U2 B D2 R’ L’ F2 B D U B U L’ B’ F’

Memorització

En la meva opinió, aquesta és la part més difícil a l'hoa de fer Blindfold, ja que d'això depen tota la resolució. Tenir el cub ben memoritzat separa una resolució exitosa d'un DNF.
Bé, anteriorment he mencionat que la resolució es dividia en 4 etapes; per lògica, a la memorització del cub l'objectiu és saber com farem cadascuna de les 4 etapes. Lordre de memorització de cada etapa és arbitrari, i cada persona memoritza de la manera que se li fa més còmode. Jo, per exemple, memoritzo primer la permutació de vèrtex, després la permutació de arestes, després la orientació de vèrtex i finalment la orientació de arestes. A continuació explicaré com memoritzar mitjançant aquest mètode (ordre en que memoritzo jo).

1. Permutació de vèrtex

   Bé, comencem donçs per la memorització dels vèrtex. Per començar em situo en la posició del vèrtex nº3, a partir de aquest vèrtex començarem el cicle. S'observa que aquest va cap a la posició nº7. Memoritzem (7). Observem cap a on va aquest i memoritzo al següent posició. Veiem que el 7 va a la posició nº1. Memoritzem (7 1). L'1 va a la posició nº3. En el moment que el 3 entra al cicle, que fins ara era (7 1), aquest cicle es tanca. A continuació anem a qualsevol vèrtex no resolt i comencem un nou cicle. Prenem ara la posició nº 2. El 2 va a la posició nº 8. Memoritzem (2 8). La peça 8 va a la posició nº 5. Memoritzem (2 8 5). La peça 5 va a la posició nº 4. Memoritzem (2 8 5 4). La peça 4 va a la posició nº 6. Memoritzem (2 8 5 4 6). La peça 6 va a la posició nº 2. Memoritzem (2 8 5 4 6 2). Com que ja hem arrivat un altre cop al 2, el cicle es tanca. Llest, ara ja no queda cap vèrtex per memoritzar, i ens han quedat dos cicles: (7 1) i ( 2 8 5 4 6 2).
   Important: La posició nº3 mai s'inclou en el primer cicle.
    

2. Permutació de arestes

   Per a les arestes es segueix el mateix procés que en la memortizació de vèrtex. És a dir, comencem per uan peça i seguim el cami que segueix el seu cicle. Comencem per la posició nº 3. Veiem que va cap a la posició nº 6. Memoritzo (6). La peça 6 va cap a pa posició nº 7. Memoritzo (6 7). La peça 7 va cap a la posició nº 10. Memoritzo (6 7 10). La peça 10 va cap a la posició nº 5. Memoritzo (6 7 10 5). La peça 5 va cap a la posició nº 12. Memoritzo (6 7 10 5 12). La peça 12 va cap a la posició nº 4. Memoritzo (6 7 10 5 12 4). La peça 4 va a la posició nº 8. Memoritzo (6 7 10 5 12 4 8). La peça 8 va cap a la posició nº 11. Memoritzo (6 7 10 5 12 4 8 11). La peça 11 va cap a la posició nº 1. Memoritzo (6 7 10 5 12 4 8 11 1). La peça 1 va cap a la posició nº 3, per tant dono per tancat el cicle. Encara falten peces per memoritzar. Vaig a la posició nº 2. Memoritzo (2). La peça 2 va cap a la posició nº 9. Memoritzo (2 9). La peá 9 va cap a la posició nº 2. Memoritzo (2 9 2). Es tanca el cicle. Llest, tota la permutació de arestes memoritzada, i al final ens han quedat 2 cicles: (6 7 10 5 12 4 8 11 1) (2 9 2).
   Important: El 3 no s'inclou al primer cicle, passa igual que amb els vèrtex.
    

3. Orientació de vèrtex

   La memorització de vèrtex sempre la faig visual. Simplement em situo a la primera capa i veig que tant al peça nº 1 com la peça nº 3 necessiten un canvi en sentit horari. A la capa inferior veig que tots els vèrtex estan mal orientats. Tots necessiten un canvi en sentit horari. En total tinc 6 vèrtex que necessiten un canvi de orientació en sentit horari, i son els següents: (1 3 5 6 7 8).
    

4. Orientació de arestes

   La memortizació de arestes la faig igual que la de vèrtex, visualment. Aquí simplemtn observo quines arestes estan mal orientades.
   A la primera capa veig que les arestes 2, 3 i 4 estan mal orientades. A la segona capa observo que les arestes 5, 7 i 8 estan mal orientades. I a la última capa veig que les arestes 10 i 12 estan mal orientades. Daquesta manera les meves arestes mal orientades son: (2 3 4 5 7 8 10 12)
    

Execució

Per fi hem arrivat a la fase de resolució. Amb aquest mètode, aquesta etapa és per a mi la mes senzilla de totes. Aquesta fase comença sempre amb la orientació i conclou amb la de permutació.

1. Orientació de arestes (2 3 4 5 7 8 10 12)

   Si fem el moviment L' aconseguirem que al aresta nº 5 es coloqui a la posició de la nº 1. D'aquesta manera el que aconseguirem serà tenir 4 arestes mal orientades a la mateixa capa. Bé, donçs apliquem l'algorisme M U M U M U M U M’ U M’ U M’ U M’ U. A continuació fem el moviment L per a retorna la peça nº 5 a la seva posició.

   Continuem. Segueixo amb les peces 7 i 8, que són oposades. A la secció d'algorismes vaig colocar un algorisme per a intercanviar 2 arestes oposades. Bé, donçs fem L R' U per a col·locar-les. Apliquem l'algorisme M U M U M U2 M’ U M’ U M’ U2. Posteriorment fem U' R L'.

   Finalment, ens queden les peces 10 i 12.  Col·loquem les peces amb R2 L2 U i apliquem l'algorisme M U M U M U2 M’ U M’ U M’ U2. Realitzem el moviment invers, U' L2 R2 i ja estan totes les arestes ben orientades.
    

2. Orientació de vèrtex (1 3 5 6 7 8 ) CW (sentit horari)

   Comencem per resoldre el vèrtex 6 i canviar la orientació del vèrtex 1. Fem R per portar el vèrtex 6 a la posició 2 i apliquem l'algorisme R’ D R D’ R’ D R U’ R’ D’ R D R’ D’ R U. Fem R' per a retornar a la posició inicial. Ara fem z2 per a veure la capa inferior a la capa superior. Fem l'algorisme per canviar 3 vèrtex en sentit horari (Considerar que A= (R’ D R D’)2) A U A U A U2.
   Tornem a fer z2 per retornar el cub a la seva posició. Per últim només falta canviar el vèrtex 1 i el 3. Fem y' per a col·locar-nos el cub, i apliquem l'algorisme per a intercanviar dos vèrtex oposats amb orientació oposada: R’ D’ R D R’ D’ R U2 R’ D R D’ R’ D R U2. Fem y per a retornar a la posició inicial. Els vèrtex ja estan orientats.
    

3. Permutació de vèrtex – (7 1) (2 8 5 4 6 2)

   Explico rapidament el que es preten fer en aquest pas. (7 1) significa que es portarà el vèrtex 7 a la posició 2, farem la permutació "T" i retornarem el 7 a la seva posició, per a posteriorment fer el mateix amb el 1: portar-lo a la posició 2, fer la permutació "T" i després retornar-lo a la posició 1. Per a portar cada un dels vèrtex a la posició 2 s'utilitza una serie de petits algorismes que mantenen tant la orientació com la posició dels vèrtex necessaris, per la qual cosa, si no es té molta experiència, es recomana fer-los com escriuré a continuació:
   1: F2 D' F2
   2: No fa falta ja que és aquí on estem portant les peces.
   3: No fa falta ja que és aquí on estem enmagatzeman les peces.
   4: L2 F2 L2
   5: F2
   6: D' F2
   7: D2 F2
   8: D F2
   Així donçs, per a portar un dels vèrtex a la posició 2 s'aplica un dels moviments esmentats, després es fa la permutació "T" i per a retornar la peça a la seva posició, es fa el moviment invers al que hem fet previament. Exemple: porto la peça 1 a la posició 2 amb el moviment F2 D' F2, faig la "T" i després faig l'invers per a retornar la peça 1 a la seva posició, que seria F2 D F2.
   Continuem amb la resolució del cub. Hem de el primer cicle és (7 1). El primer, portar la peça 7 a la posició 2 amb l'
   algorisme D2 F2, fer la T permutation i després tornar la peça amb l'algorisme F2 D2. Seguim amb la peça 1. Apliquem F2
   D 'F2 per portar-la a la posició 2, fem la T permutation, i després tornem la peça amb l'algoritme F2 D F2. Seguim
   amb el següent cicle. Hem de comença amb 2. Atès que el 2, per obvietat ja és a la posició 2, simplement apliquem
   la T permutation. Després seguim amb el 8. Apliquem D F2 per portar-la a la posició 2, després apliquem la T permutation, i la
   tornem amb F2 D '. Després aplicar F2 per portar el vèrtex 5 a la posició 2, T permutation, i després F2 per tornar. Després
   fem L2 F2 L2 per portar la peça 4 a la posició 2, apliquem T permutation, i tornem amb L2 F2 L2. Portem la peça 6
   a la posició 2 amb l'algoritme D 'F2, T permutation, i tornem amb F2 D. Finalment, només queda el 2 que tanca el cicle.
   Com ja és a la posició 2, només apliquem la T permutation.

   Nota important: En aquest cas, ens van tocar cicles parells, és a dir, tenim en total 8 números. En cas de no tenir un nombre
   parell, per exemple, tenint 7 números en el cicle, cal aplicar al final una T permutation per eliminar la "paritat".
   Amb el temps això es fa mecànic.

4. Permutació d'arestes - (6 7 10 5 12 4 8 11 1) (2 9 2)
   Similar al que succeeix en els vèrtexs, per als arestes tenim una sèrie de moviments que aplicarem de la mateixa manera per
   anar resolent el cicle. Els moviments són els següents, per a cadascuna de les arestes:
   1: No cal ja que aquí és on estem portant les peces
   2: R2 U R2
   3: No cal ja que d'aquí estem traient les peces
   4: R2 U 'R2
   5: d 'L
   6: d 'L'
   7: dL
   8: d l '
   9: D 'L2
   10: D2 L2
   11: D L2
   12: L2
   Comencem amb el cicle. En aquesta fase, les arestes els hem de portar a la posició d'arestes 1. Portem primer la aresta 6
   a la posició 1, apliquem d 'l', fem la T permutation, i després vam tornar el 6 a la seva posició aplicant el invers, L d.
   Portem la 7 a la posició 1 aplicant d L, T permutation, i després vam tornar aplicant l 'd'. Portem la 10 a la posició 1
   aplicant D2 L2, T permutation, i tornem amb L2 D2. Portem el 5 a la posició 1 amb d 'L, T permutation, i tornem amb
   L 'd. Portem el 12 a la posició 1 aplicant L2, T permutation, i tornem amb L2. Portem la peça 4 a la posició 1
   aplicant R2 U 'R2, T permutation, i tornem amb R2 U R2. Portem la peça 8 a la posició 1 amb d l ', T permutation, i
   tornem amb L d '. Portem la peça 11 a la posició 1 amb D L2, T permutation, i tornem amb L2 D '. La peça 1 està en
   posició, apliquem la T permutation, i passem amb el següent cicle. Portem la peça 2 a la posició 1 amb l'algoritme R2 U
   R2, T permutation, i tornem amb R2 U 'R2. Després portem la 9 a la posició 1 amb D 'L2, T permutation, i tornem amb L2
   D. Finalment portem el vèrtex 2 a la posició 1 aplicant R2 U R2, T permutation, i tornem amb R2 U 'R2. Llest, ¡el cub
   està resolt! O almenys hauria de estar-ho si has fet tot pas a pas. ;)
   

Comentari Final

Amb tot el que he explicat en aquestes pàgines, ja hauries de ser capaç de fer el cub a cegues, en cas de no ser així, llegeix
tot de nou posant molta atenció. Al final, és més fàcil del que podria semblar. = D

Agraïments

Bé, agraïment especial a la meva xicota, que aguanta coses com aquesta = P gràcies per aguantar la meva afició al cub amor = D.
Als meus amics, que em van motivar a fer el manual.
A Cinthya que ha promogut el meu nom i vídeos.
A Uriel ja Ricardo, vaja, que els dec molt pel que fa als meus temps.
A l'equip de Rubikaz, a Carlos, per no posar traves a l'ús de la seva pàgina per a alguns algorismes.
A tots els que llegeixen el tutorial;)
Dubtes / Comentaris:
Us deixo el meu msn: beatles_chente@hotmail.com

Salutacions;)